Οι Πυθαγόρειοι είχαν όλα τα «κλειδιά». Στο ρυθμό της κοσμικής μουσικής που πρώτοι «άκουσαν» οι μαθηματικοί του 6ου π.Χ. αιώνα εξακολουθεί να χορεύει η σύγχρονη Κοσμολογία.
Ένας Έλληνας καθηγητής Μουσικής και Πληροφορικής, με πανεπιστημιακές σπουδές στη Φυσική και ερευνητικό έργο στα Πυθαγόρεια Μαθηματικά απέδειξε ότι η «αρμονία σφαιρών», η περίφημη πυθαγόρεια θεωρία, έχει ακριβή εφαρμογή σε όλους τους γνωστούς μας σήμερα πλανήτες.
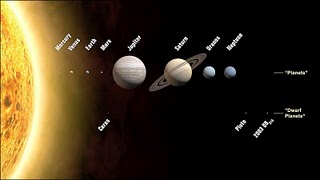
Ο πρώην πρόεδρος της Ένωσης Ελλήνων Φυσικών, διευθυντής του Τομέα Τεχνολογίας Ήχου, Μουσικοπαιδαγωγικής και Βυζαντινής Μουσικολογίας της Φιλοσοφικής Σχολής του Πανεπιστημίου Αθηνών Χαράλαμπος Σπυρίδης ανακοινώνει στο επιστημονικό συμπόσιο «Φιλοσοφία και Κοσμολογία» τους αριθμούς που εκφράζουν σε αστρονομικές μονάδες τις αποστάσεις των πλανητών από τον Ήλιο πιάνοντας το νήμα από τους Πυθαγορείους.
Ο κ.Σπυρίδης διατυπώνει «μια καθολική, εξαιρετικά απλή και κομψή σχέση» που εμπεριέχει μόνον τους αριθμούς 1, 2, 3, 4 της «ιερής τετρακτύος» των Πυθαγορείων και το άθροισμά τους, τον «τέλειο» αριθμό 10.
Η «τετρακτύς» ήταν η βάση της πυθαγόρειας διδασκαλίας που πρέσβευε ότι οι ήχοι των ουράνιων σωμάτων συνθέτουν μία κοσμική μουσική, γιατί οι αποστάσεις και οι ταχύτητες των πλανητών και των απλανών αστέρων διέπονται από τους ίδιους αριθμητικούς λόγους που παράγουν και τη συμφωνία των ήχων.
Οι συμφωνίες των ήχων που παράγουν αρμονικό αποτέλεσμα έχουν μορφή απλών αριθμητικών σχέσεων. Επομένως κατά τους Πυθαγόρειους το μυστικό της μουσικής και της κοσμικής αρμονίας κρύβεται στις σχέσεις των τεσσάρων πρώτων φυσικών αριθμών (1, 2, 3, 4).
Ο Πυθαγόρας είναι ο πρώτος φιλόσοφος που συνδέει την Αστρονομία με τη Μουσική, υποστηρίζοντας ότι στο αρμονικό και σφαιρικό σύμπαν τα πάντα διέπονται από απλούς νόμους, που μπορούν να εκφρασθούν με τους αριθμούς της «ιερής τετρακτύος».
Με τη θεωρία της αρμονίας των σφαιρών που συνδυάζει την κοσμική αρμονία με τη μουσική αρμονία, ο μεγάλος φιλόσοφος επιχείρησε να εξηγήσει τη θέση και την κίνηση των πλανητών στον ουράνιο θόλο. Χρησιμοποιώντας μουσικούς όρους, δηλαδή εύφωνα μουσικά διαστήματα, καθόρισε υπό μορφήν κλίμακας τις μεσοπλανητικές αποστάσεις.
Ακολούθως, αντιστοιχίζοντας τα μουσικά διαστήματα σε μετρικές αποστάσεις, κατόρθωσε πρώτος να υπολογίσει σε Δελφικά στάδια τις μεσοπλανητικές αποστάσεις των «ουρανίων γεννητών», όπως ονόμασε τα ουράνια σώματα ο Πλάτωνας παίρνοντας το νήμα από τον Πυθαγόρα.
Ο Πυθαγόρας τον 6ο π.Χ. αιώνα δέχθηκε ότι η μουσική απόσταση μεταξύ Γης και Σελήνης είναι ένας τόνος και η μετρική απόσταση μεταξύ τους είναι 126.000 Δελφικά στάδια, δηλαδή 22.371.300 μέτρα.
Σχεδόν 24 αιώνες μετά δύο Γερμανοί αστρονόμοι, ο Γιόχαν Μπόντε και ο Τίτιους, προσδιορίζουν τις θέσεις των γνωστών τότε πλανητών του ηλιακού μας συστήματος με ικανοποιητική ακρίβεια. Η εμπειρική ανακάλυψή τους, ανερμήνευτη μέχρι σήμερα, έμεινε γνωστή ως ο κανόνας Μπόντε-Τίτιους.
Ο κανόνας των Γερμανών αστρονόμων έπαψε να δίνει αξιόπιστα αποτελέσματα όταν επιχειρήθηκε να εφαρμοστεί στους «νεότερους» πλανήτες και στη ζώνη πέρα από τον Πλούτωνα, μία από τις συναρπαστικότερες περιοχές του ηλιακού συστήματος, γεμάτη αντικείμενα από βράχο και πάγο που περιστρέφονται γύρω από τον Ήλιο σε τεράστιες αποστάσεις.
Ο καθηγητής Σπυρίδης, μελετώντας επί σειρά ετών τις πλατωνικές απόψεις «περί των θείων γεννητών», τις οποίες συγκέρασε με την «αρμονία των σφαιρών» του Πυθαγόρα, ανακάλυψε ότι ο κανόνας των δύο Γερμανών αστρονόμων του 18ουαιώνα αποτελεί μία μαθηματική έκφραση της πυθαγόρειας μουσικής των σφαιρών.
Στο συμπόσιο του Πανεπιστημίου Αθηνών θα αποδείξει ότι κατάφερε να επεκτείνει την ακριβή εφαρμογή της πυθαγόρειας θεωρίας σε όλους τους γνωστούς πλανήτες, ενώ θα υποδείξει συγκεκριμένες θέσεις «πλανητικών» αντικειμένων μετά τον Πλούτωνα.
Όπως δήλωσε στον «Ε.Τ.» «Η γέφυρα που κατασκευάσθηκε και συνδέει τον κόσμο των αστρονόμων με τον κόσμο των μουσικών διασφαλίζει την αιωνιότητα μιας συμπαντικής αρμονίας σε πλήρη εξέλιξη, η οποία θα προσδιορίσει το χωροχρόνο μέσω των γνώσεων της Αστρονομίας και της Μουσικής στην εκάστοτε εποχή».