Ο «χρυσός» αριθμός Φ
Ο Πυθαγόρας πρώτος παρατήρησε ότι τα φυτά και τα ζώα δεν μεγαλώνουν τυχαία, αλλά σύμφωνα με ακριβείς μαθηματικούς κανόνες. Δεν είναι τυχαία δηλαδή τα όμορφα σχέδια των λουλουδιών.
Οι αρχαίοι Έλληνες βρήκαν ότι τα σχέδια των λουλουδιών βασίζονται σε γεωμετρική αναλογία. Επίσης η ακολουθία κάνει την εμφάνισή της στη διάταξη των φύλων γύρω από το μίσχο.
Εμφανίζεται ακόμα και στην ανάπτυξη των βελόνων αρκετών ειδών ελάτου, καθώς επίσης και στη διάταξη των πετάλων στις μαργαρίτες και τα ηλιοτρόπια. Μερικά κωνοφόρα δένδρα παρουσιάζουν τη σειρά αριθμών στη δομή της επιφάνειας των κορμών τους, ενώ τα φοινικόδεντρα στους δακτυλίους των κορμών τους.
Με τις πράξεις που έκανε ο Ιταλός μαθηματικός Fibonacci, ο οποίος ήταν πολύ γνωστός στην εποχή του και αναγνωρίζεται και σήμερα, βρήκε ότι το κλειδί της ομορφιάς είναι η αναλογία 1 προς 1,618, ο αριθμός Φ.
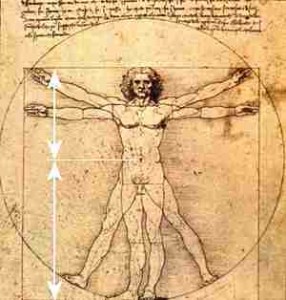
Για παράδειγμα, η σχέση από το πάτωμα ως τον ομφαλό και από εκεί στο κεφάλι θα είναι 1 προς Φ, αν οι αναλογίες είναι ιδανικές.
Σχέση των αναλογιών στο σώμα μας και την χρυσή τομή.
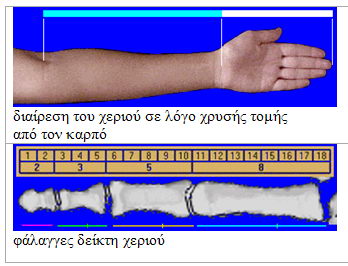
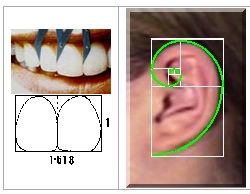
Επίσης, το πλάτος του στόματος είναι Φ φορές το πλάτος της μύτης.
Ο Χρυσός αριθμός θεωρούταν από τους αρχαίους Έλληνες ως η θεϊκή αναλογία όπου η εφαρμογή του σε καλλιτεχνικά δημιουργήματα και κατασκευές οδηγούσε σε «άριστα» και «ωραία» αποτελέσματα.
Μετά από πάρα πολλά χρόνια ο Fibonacci ανακάλυψε μία ακολουθία αριθμών που είχαν την ιδιότητα να εμφανίζουν την χρυσή αναλογία. 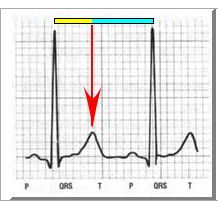
Ομοίως και για οποιαδήποτε άλλη ακολουθία με σημείο εκκίνησης οποιονδήποτε αριθμό.
ΟΙ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΑΡΙΘΜΟΥ Φ
Το Φ στην αρχιτεκτονική
Η πρόσοψη του Παρθενώνα αποτελεί ένα παράδειγμα χρήσης της χρυσής τομής(Φ) στην αρχιτεκτονική. Δεν είναι γνωστό όμως αν οι αναλογίες δόθηκαν διαισθητικά ή με γνώση του αριθμού Φ.
Ο τριγωνισμός, μια άλλη μέθοδος συγκρότησης ρυθμικών καμβάδων με βάση ορισμένα προνομιούχα τρίγωνα, γνώρισε τη μεγαλύτερη διάδοσή του τον περασμένο αιώνα.
Αυτά είναι: (1)το πυθαγόρειο, δηλαδή το ορθογώνιο με σχέση πλευρών 3:4:5, (2) το αιγυπτιακό, δηλαδή το ισοσκελές με αναλογία βάσης προς ύψος 8:5, (3) το ισοσκελές με γωνία κορυφής 36 μοίρες, που αποτελεί τη μονάδα του κανονικού δεκαγώνου, και έχει σχέση πλευράς προς βάση Φ (1,618, ο γνωστός χρυσός αριθμός) και τέλος (4) το ισόπλευρο, που αποτελεί τη μονάδα του εξαγώνου.
Τέτοιες μεθόδους επαλήθευσης συναντά κανείς στα αρχιτεκτονικά έργα του μοντέρνου κινήματος, Le Corbusier, Bauhaus κλπ.
Το Φ στην τέχνη
Αργότερα ο Leonardo Da Vinci ζωγράφισε το πρόσωπο της Mona Lisa ώστε αυτό να χωράει τέλεια σε ένα χρυσό ορθογώνιο και δόμησε τον υπόλοιπο πίνακα γύρω από το πρόσωπο χωρίζοντάς τον επίσης σε χρυσά ορθογώνια.
Κατά την Αναγέννηση οι καλλιτέχνες άρχισαν να επιστρέφουν στα κλασσικά θέματα της αρχαιότητας για τις εμπνεύσεις τους και τις τεχνικές τους.
Θα μπορούσαμε για παράδειγμα να αναφέρουμε τους Michelangelo (1475-1564) καιRaphael (1483-1530) οι οποίοι επανέφεραν στις συνθέσεις τους την χρυσή τομή.
Ο ομφαλός διαιρεί το σώμα του Δαβίδ του Michelangelo σε λόγο χρυσής τομής.
Η πιο πρόσφατη αναζήτηση για μία «γραμματική» στην τέχνη οδήγησε μοιραία τους σύγχρονους καλλιτέχνες στην χρήση της χρυσής τομής.
Η Παρέλαση του Γάλλου νέο-ιμπρεσιονιστή καλλιτέχνη Seurat (1859 – 1891), που χαρακτηρίζεται από το γνωστό του στυλ με τις άπειρες κουκκίδες, περιέχει πλήθος παραδειγμάτων χρυσών αναλογιών.
Σύμφωνα με έναν εμπειρογνώμονα τέχνης, ο Seurat «επιτέθηκε σε κάθε καμβά του με τη χρυσή αναλογία».
Τα χρυσά ορθογώνια είναι πολύ εμφανή στους Λουόμενούς του.
Ο Μυστικός Δείπνος του SalvadorDali (1904-1989) πλαισιώνεται από ένα χρυσό ορθογώνιο.
Χρυσοί λόγοι χρησιμοποιήθηκαν για να καθορίσουν την θέση κάθε φιγούρας ενώ ο θόλος του δωματίου σχηματίζεται από τις έδρες κανονικού δωδεκάεδρου που όπως είδαμε είναι ένα από τα στερεά που συνδέεται άμεσα με την χρυσή τομή.
Μουσική
Να αναφέρουμε τέλος πως και η μουσική δεν έμεινε ανεπηρέαστη από την χρυσή τομή.
Αγνοούμε όμως αν αυτό έγινε συνειδητά ή ασυνείδητα.
Παρατηρούμε και εδώ στα έργα των μεγάλων συνθετών όπως του Μότσαρτ ή του Μπετόβεν να υπάρχει μία διαίρεση των συνθέσεων σε λόγους χρυσής τομής.
Το Φ στη Γεωμετρία των Fractals
Ένας καλλιτέχνης του 15ου αιώνα που παρήγαγε ένα fractal αντικείμενο. Θεωρούμε ένα κανονικό πεντάγωνο και στην κάθε πλευρά του ας προσαρτήσουμε από άλλο ένα ίδιο κανονικό πεντάγωνο.
Με τον τρόπο αυτόν δημιουργούνται μέσα έξι νέα πεντάγωνα στα οποία εφαρμόζοντας την ίδια διαδικασία λαμβάνουμε ένα fractal απίστευτο για την εποχή του.
Από υπολογισμούς μπορούμε να δούμε ότι ο λόγος των πλευρών κάθε ισοσκελούς τριγώνου βρίσκεται στη χρυσή τομή.
Το Φ στη Βίβλο του Ισλάμ
Η λέξη Κοράνι, πιο σωστά στα Αραβικά Κουράν – Qur’an, προέρχεται από το ρήμα κάρα’α – qara’a που σημαίνει, απαγγέλλω κι αποτελείται από 114 κεφάλαια (Σούρα).
Ο αριθμός 114 είναι διαιρετέος με το 19, ήτοι 19*6=114.
Το 114 προκύπτει από τη διαίρεση του κύκλου με το π, ήτοι 360/π, όπου π=3,14159 και το 19 εκτός του ότι είναι ο Μετωνικός Αριθμός, προκύπτει επίσης σαν δεκαπλάσιο του π/Φ, όπου Φ=1,618034
Το Φ στον άνθρωπο
Το ανθρώπινο σώμα έχει δομηθεί και αναπτύσσεται σε αναλογίες Φ.
Δεν είναι τυχαίο ότι πολλές «ανατολίτικες θρησκείες» και κινήματα στα πλαίσια της διδασκαλίας τους για διαλογισμό και την «αυτοσυγκέντρωση και στο λεγόμενο «γιόγκα» η στάση του ανθρώπινου σώματος γίνεται κατά αυτό τον τρόπο έτσι ώστε τα «κεντρικά – κομβικά» σημεία του σώματος να βρίσκονται σε αναλογίες Φ.
Αν θέλει κανείς να δει ένα χρυσό ορθογώνιο αρκεί να κοιτάξει μια πιστωτική κάρτα το σχήμα της οποίας είναι ακριβώς αυτό.
Τέλος υπάρχουν καταγραφές που μιλούν για την ύπαρξη του Φ στην δομή του DNA.
Φυσικά η επιρροή του λόγου χρυσής τομής ήταν τεράστια σε όλο τον αρχαίο ελλαδικό χώρο.
ΕΙΣΑΓΩΓΗ
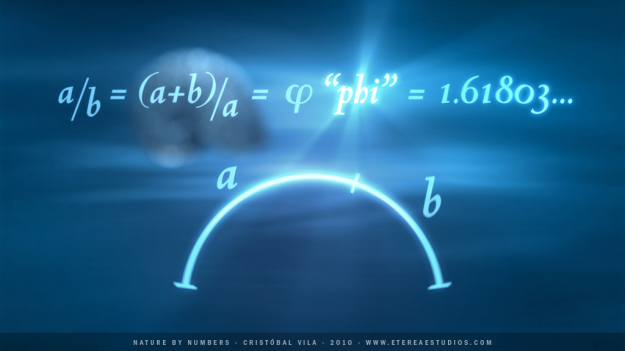
 Τα πρώτα πραγματικά αριθμητικά συστήματα είναι, ωστόσο, πολύ νεότερα. Ανάμεσα στους πρώτους πολιτισμούς που κατείχαν τόσο τη γλώσσα όσο και τους υπολογισμούς ήταν οι αρχαίοι Βαβυλώνιοι της Μεσοποταμίας, στο σημερινό Ιράκ.
Τα πρώτα πραγματικά αριθμητικά συστήματα είναι, ωστόσο, πολύ νεότερα. Ανάμεσα στους πρώτους πολιτισμούς που κατείχαν τόσο τη γλώσσα όσο και τους υπολογισμούς ήταν οι αρχαίοι Βαβυλώνιοι της Μεσοποταμίας, στο σημερινό Ιράκ. Σ’ ένα θεσιακό αριθμητικό σύστημα, η αξία κάθε ψηφίου εξαρτάται από τη θέση του ψηφίου αυτού στον αριθμό. Για παράδειγμα, προτιμάμε να έχουμε 1500 ευρώ αντί για 1050 ή 1005, γιατί η μετακίνηση του 5 προς τα δεξιά μειώνει την τιμή του.
Σ’ ένα θεσιακό αριθμητικό σύστημα, η αξία κάθε ψηφίου εξαρτάται από τη θέση του ψηφίου αυτού στον αριθμό. Για παράδειγμα, προτιμάμε να έχουμε 1500 ευρώ αντί για 1050 ή 1005, γιατί η μετακίνηση του 5 προς τα δεξιά μειώνει την τιμή του.

Ανάμεσα στα χιλιάδες σωζόμενα ανάγλυφα, μνημεία και αγάλματα της αρχαίας Βαβυλώνας, ορισμένοι (όπως το ανάγλυφο «Πληγωμένη λέαινα», του 650 π.Χ.) εγγράφονται με ελάχιστες αποκλίσεις σε ένα ορθογώνιο παραλληλόγραμμο που ο λόγος των διαστάσεών του ισούται με φ. Με βάση αυτό, πολλοί ιστορικοί της τέχνης και ερασιτέχνες αρχαιολόγοι έχουν υποστηρίξει από παλιά ότι οι Βαβυλώνιοι γνώριζαν τη χρυσή αναλογία. Κατά πάσα πιθανότητα, όμως, πρόκειται για εσφαλμένη αντίληψη. Οι σοβαρότερες έρευνες για την αρχαιότητα αμφισβητούν εδώ και δεκαετίες την τάση των αριθμολόγων αποκρυφιστών να βλέπουν παντού το φ. Οι σκεπτικιστές επισημαίνουν ότι μπορούμε να βρούμε άπειρους διαφορετικούς αριθμούς σχεδόν σε κάθε αντικείμενο. Αν μετρήσει κανείς τις διαστάσεις μιας τηλεόρασης και εφαρμόσει σ’ αυτές τις 4 πράξεις της αριθμητικής, μπορεί να εξαγάγει όποιο αποτέλεσμα θέλει (μεταξύ αυτών και το φ). Όμως, δεν μπορεί με γνώμονα αυτούς τους υπολογισμούς να συμπεράνει ότι ο κατασκευαστής της τηλεόρασης χρησιμοποίησε συνειδητά το φ.

Ο ΜΑΘΗΜΑΤΙΚΟΣ ΕΥΚΛΕΙΔΗΣ
Ο Ευκλείδης συγκέντρωσε το μεγαλύτερο μέρος των τότε πρακτικών μαθηματικών γνώσεων σε 13 βιβλία με το γενικό τίτλο «Στοιχεία», τα οποία αποτέλεσαν έκτοτε υπόδειγμα για κάθε μαθηματικό. Τα «Στοιχεία» έχουν γνωρίσει πάνω από 1.000 εκδόσεις από την πρώτη τους εκτύπωση στο τυπογραφείο του Γουτεμβέργιου, εδώ και περίπου 500 χρόνια. Είναι πιθανότατα το πιο πολυδιαβασμένο βιβλίο στο Δυτικό κόσμο, μετά τη Βίβλο. 
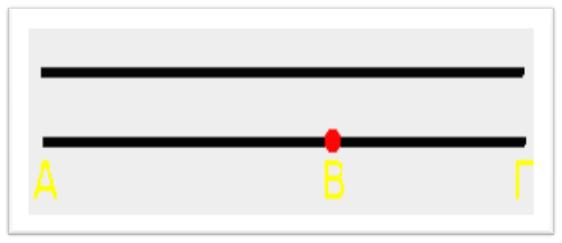
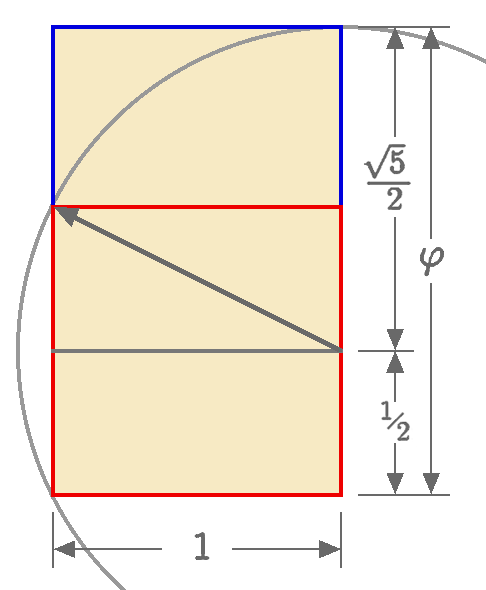
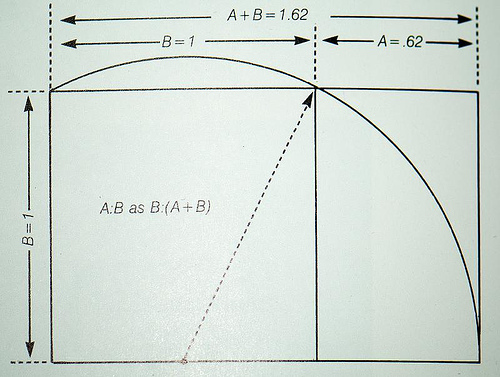
Με τη βοήθεια αυτών των θεμελιωδών αξιωμάτων, ο Ευκλείδης κατάφερε να αποδείξει την ισχύ όλης της γεωμετρίας των κύκλων, των τριγώνων, των ορθογωνίων παραλληλογράμμων κλπ., την οποία διδάσκονται ακόμα και σήμερα τα παιδιά στα σχολεία. Οι σημερινοί μαθηματικοί εξάγουν κι αυτοί τα συμπεράσματά τους στηριζόμενοι σε αξιώματα.  Το έργο του Ευκλείδη αποτέλεσε ορόσημο για τα μαθηματικά. Με το καινούργιο του εργαλείο, ο αρχαίος μαθηματικός κατάφερε να προσεγγίσει τη χρυσή αναλογία. Ο αριθμός φ αντλεί τον ορισμό του από τη λεγόμενη χρυσή τομή.Η αφετηρία είναι γεωμετρική: ο Ευκλείδης παίρνει ένα ευθύγραμμο τμήμα (ΑΒ) και το διαιρεί σε δύο τμήματα (ΑΓ) και (ΓΒ). Η χρυσή τομή είναι εκείνο το σημείο (Γ) που διαιρεί το ευθύγραμμο τμήμα (ΑΒ) στα δυο τμήματα, έτσι ώστε το πηλίκο του (ΑΒ) προς το μεγαλύτερο τμήμα (ΑΓ) να είναι ίσο με το πηλίκο του μεγαλύτερου τμήματος (ΑΓ) προς το μικρότερο (ΓΒ). Η αναλογία αυτή λέγεται «χρυσή αναλογία» και σύμφωνα με τον ορισμό του Ευκλείδη, υπολογίζεται ότι έχει αριθμητική τιμή 1,618…, δηλαδή ότι το μεγαλύτερο τμήμα θα έχει πάντα 1,618… φορές μεγαλύτερο μήκος από το μικρότερο. Τα δεκαδικά ψηφία είναι άπειρα και η ακολουθία τους δεν επαναλαμβάνεται.
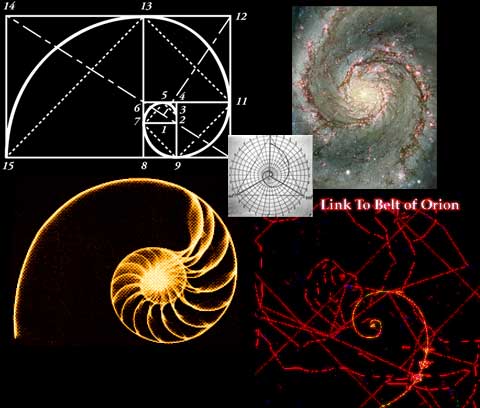
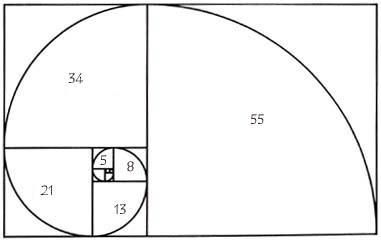
Το έργο του Ευκλείδη αποτέλεσε ορόσημο για τα μαθηματικά. Με το καινούργιο του εργαλείο, ο αρχαίος μαθηματικός κατάφερε να προσεγγίσει τη χρυσή αναλογία. Ο αριθμός φ αντλεί τον ορισμό του από τη λεγόμενη χρυσή τομή.Η αφετηρία είναι γεωμετρική: ο Ευκλείδης παίρνει ένα ευθύγραμμο τμήμα (ΑΒ) και το διαιρεί σε δύο τμήματα (ΑΓ) και (ΓΒ). Η χρυσή τομή είναι εκείνο το σημείο (Γ) που διαιρεί το ευθύγραμμο τμήμα (ΑΒ) στα δυο τμήματα, έτσι ώστε το πηλίκο του (ΑΒ) προς το μεγαλύτερο τμήμα (ΑΓ) να είναι ίσο με το πηλίκο του μεγαλύτερου τμήματος (ΑΓ) προς το μικρότερο (ΓΒ). Η αναλογία αυτή λέγεται «χρυσή αναλογία» και σύμφωνα με τον ορισμό του Ευκλείδη, υπολογίζεται ότι έχει αριθμητική τιμή 1,618…, δηλαδή ότι το μεγαλύτερο τμήμα θα έχει πάντα 1,618… φορές μεγαλύτερο μήκος από το μικρότερο. Τα δεκαδικά ψηφία είναι άπειρα και η ακολουθία τους δεν επαναλαμβάνεται.  Κατά τον ίδιο τρόπο, αποκαλούμε ένα ορθογώνιο παραλληλόγραμμο «χρυσό», όταν το πηλίκο της μεγαλύτερης προς τη μικρότερη πλευρά του ισούται με φ. Αυτό το ορθογώνιο έχει μια ιδιότητα που το ξεχωρίζει από όλα τα άλλα: αν αφαιρέσουμε από τη μια πλευρά το μεγαλύτερο δυνατό τετράγωνο, απομένει ένα καινούργιο ορθογώνιο, που είναι επίσης χρυσό, και αυτό μπορεί να συνεχιστεί επ’ άπειρον. Αν ενώσει κανείς με μια καμπύλη τις κορυφές όλων αυτών των ορθογωνίων, που είναι και χρυσές τομές, σχηματίζεται μια λογαριθμική έλικα. Αυτή ακριβώς η έλικα υπάρχει παντού στη φύση. Για παράδειγμα, στο κέλυφος των σαλιγκαριών, στο όστρακο των ναυτίλων και στην ιδιόμορφη ελικοειδή διάταξη που σχηματίζεται από τους σπόρους των ηλίανθων.
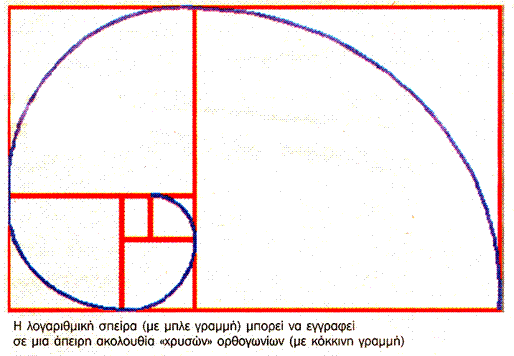
Κατά τον ίδιο τρόπο, αποκαλούμε ένα ορθογώνιο παραλληλόγραμμο «χρυσό», όταν το πηλίκο της μεγαλύτερης προς τη μικρότερη πλευρά του ισούται με φ. Αυτό το ορθογώνιο έχει μια ιδιότητα που το ξεχωρίζει από όλα τα άλλα: αν αφαιρέσουμε από τη μια πλευρά το μεγαλύτερο δυνατό τετράγωνο, απομένει ένα καινούργιο ορθογώνιο, που είναι επίσης χρυσό, και αυτό μπορεί να συνεχιστεί επ’ άπειρον. Αν ενώσει κανείς με μια καμπύλη τις κορυφές όλων αυτών των ορθογωνίων, που είναι και χρυσές τομές, σχηματίζεται μια λογαριθμική έλικα. Αυτή ακριβώς η έλικα υπάρχει παντού στη φύση. Για παράδειγμα, στο κέλυφος των σαλιγκαριών, στο όστρακο των ναυτίλων και στην ιδιόμορφη ελικοειδή διάταξη που σχηματίζεται από τους σπόρους των ηλίανθων.
Η ανακάλυψη των άρρητων αριθμών δημιούργησε στους κύκλους των σοφών της αρχαίας Ελλάδας, ούτε λίγο ούτε πολύ, μια φιλοσοφική κρίση, διότι οι αριθμοί αυτοί θεωρήθηκαν σαν ένα τρομακτικό λάθος στην κατασκευή του σύμπαντος. Η σχολή των Πυθαγορείων είχε δημιουργήσει ένα φιλοσοφικό θρησκευτικό σύστημα με βάση τους ακέραιους αριθμούς. Για τους Πυθαγόρειους, μάλιστα, οι αριθμοί είχαν φυσική οντότητα στον κόσμο. Σύμφωνα με ένα ιστορικό ανέκδοτο, ο ιδρυτής του κινήματος Πυθαγόρας είχε κάποτε ακούσει δυο σιδεράδες να σφυροκοπούν πυρακτωμένα σίδερα. Οι τόνοι διέφεραν μεταξύ τους κατά διαστήματα ογδόης (οκτάβες), πέμπτης και τετάρτης και γι’ αυτό ηχούσαν αρμονικά. Οι σιδεράδες είχαν πολλά σφυριά και οι τονικές διαφορές οφείλονταν στο διαφορετικό βάρος των σφυριών αυτών. Μια οκτάβα, δηλαδή ένα διάστημα 8 βαθμίδων ανάμεσα σε δύο διαδοχικές ίδιες νότες της επτάφθογγης κλίμακας, προέκυπτε από το χτύπημα δύο σφυριών που η σχέση τους ως προς το βάρος ήταν 2:1, για παράδειγμα, ζύγιζαν αντίστοιχα 12 και 6 κιλά (ή κάτι ανάλογο σε οποιαδήποτε μονάδα βάρους). Ακόμα και για τα διαστήματα πέμπτης και τετάρτης, η αναλογία του βάρους των σφυριών μπορούσε να δοθεί με κλάσματα μικρών ακέραιων αριθμών, όπως το 3:2 και 4:3. Για τον Πυθαγόρα, η ικανότητα των ακέραιων αριθμών να παράγουν μουσική αρμονία αποτελούσε ένα ακόμα τεκμήριο της κυριαρχίας τους στο σύμπαν.
 |
| Αριθμητικό σύστημα των Μάγια |
ΟΙ ΙΝΚΑΣ ΜΕΤΡΟΥΣΑΝ ΜΕ ΚΟΜΠΟΥΣ
Οι αριθμοί μπορούν να παρασταθούν και με άλλους τρόπους εκτός των γραπτών συμβόλων, κι αυτό το απέδειξαν οι Ίνκας με το δικό τους σύστημα αρίθμησης. Σε αντίθεση με άλλους μεγάλους πολιτισμούς, οι Ίνκας δεν διέθεταν γραπτή γλώσσα. Οι κρατικοί λειτουργοί μετρούσαν κατοίκους και σοδειές με τη βοήθεια ενός αριθμητηρίου. Τα αθροίσματα «καταγράφονταν» με κόμπους σ’ ένα κατασκεύασμα από σχοινιά που λεγόταν quipu. Τα σχοινιά ήταν από μαλλί, βαμβάκι ή φυτικές ίνες και αντιπροσώπευαν, π.χ., έναν αριθμό στρατιωτών, την ποσότητα κάποιου προϊόντος σε μια αποθήκη ή τον αριθμό των φορολογουμένων σε μια πόλη. Το χρώμα του σχοινιού μαρτυρούσε το είδος της μετρούμενης ποσότητας: το άσπρο σήμαινε, για παράδειγμα, ασήμι, το κίτρινο πολεμιστές και το γκρι επαρχίες. Ένας κόμπος αναπαριστούσε μια μονάδα, δύο κόμποι, ο ένας πάνω από τον άλλον, δύο μονάδες κλπ. 
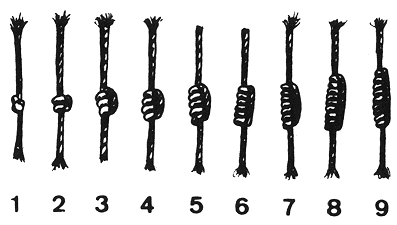
Το quipu λειτουργούσε ταυτόχρονα και σαν ημερολόγιο αλλά και σαν βοήθημα για προφορικές αφηγήσεις. Ίσως ο τρόπος ύφανσης των σχοινιών, το υλικό και οι διαφορετικών ειδών κόμποι να είχαν και αυτά κάποια σημασία, που ακόμα μας είναι άγνωστη.
Η ΕΥΡΩΠΗ ΚΡΑΤΗΣΕ ΤΑ ΡΩΜΑΪΚΑ ΨΗΦΙΑ
Οι αρχαίοι Έλληνες ήταν εξαίρετοι γεωμέτρες, που ερευνούσαν τη λογική και την εσωτερική δομή των μαθηματικών με πρωτοποριακό τρόπο. Όμως, το αριθμητικό τους σύστημα, το οποίο είχε ομοιότητες με το ρωμαϊκό, ποτέ δεν εξελίχθηκε ιδιαίτερα, ίσως επειδή η πρώιμη ανακάλυψη των άρρητων αριθμών κλόνισε το κύρος των ακεραίων. Η ανακάλυψη του νεότερου δεκαδικού συστήματος έγινε από τους Ινδούς και τα σύμβολα με τα οποία αναπαριστούμε τα ψηφία προέρχονται από τα ινδικά ψηφία brahmi, τα οποία αναπτύχθηκαν γύρω στο 500 μ.Χ. Γύρω στο 700 μ.Χ., οι Ινδοί τελειοποίησαν το δεκαδικό σύστημα αρίθμησης, περιλαμβάνοντας σ’ αυτό και το μηδέν. Επειδή ήταν ευκολότερο να γίνονται οι τέσσερις πράξεις με τα αριθμητικά ψηφία των Ινδών, παρά με τα ελληνικά ή τα βαβυλωνιακά, τα νέα αυτά ψηφία διαδόθηκαν γρήγορα στην Κίνα και στον αραβικό κόσμο. Εκεί απέκτησαν, με το πέρασμα του χρόνου, μια άλλη μορφή, αλλά οι αρχές του συστήματος παρέμειναν ίδιες. Στην Ευρώπη το ινδικό σύστημα αρίθμησης το έφεραν οι Άραβες.  Η Ευρώπη άργησε να συντονιστεί στις αλλαγές. Μόλις γύρω στο 1200, ο Ιταλός μαθηματικός Leonardo Fibonacci διέδωσε το δεκαδικό σύστημα σ’ έναν ευρύτερο κύκλο. Το γεγονός ότι ο Fibonacci ήταν αυτό που έφερε την επανάσταση στα ευρωπαϊκά μαθηματικά είχε να κάνει με την πολυπολιτισμική ανατροφή του. Ο πατέρας του, που ήταν Ιταλός πρόξενος, έστειλε το γιο του να μαθητεύσει κοντά σ’ έναν Άραβα μαθηματικό.
Η Ευρώπη άργησε να συντονιστεί στις αλλαγές. Μόλις γύρω στο 1200, ο Ιταλός μαθηματικός Leonardo Fibonacci διέδωσε το δεκαδικό σύστημα σ’ έναν ευρύτερο κύκλο. Το γεγονός ότι ο Fibonacci ήταν αυτό που έφερε την επανάσταση στα ευρωπαϊκά μαθηματικά είχε να κάνει με την πολυπολιτισμική ανατροφή του. Ο πατέρας του, που ήταν Ιταλός πρόξενος, έστειλε το γιο του να μαθητεύσει κοντά σ’ έναν Άραβα μαθηματικό.

Κατά μία ειρωνεία της τύχης, όμως, ο Fibonacci δεν έγινε γνωστός ως εισηγητής του δεκαδικού συστήματος στην Ευρώπη, αλλά για τους υπολογισμούς του σχετικά με τον πολλαπλασιασμό των κουνελιών. Σ’ έναν περίφημο , πλέον, συλλογισμό, ο Fibonacci υπέθεσε ότι δυο κουνέλια είναι σε θέση να αρχίσουν να ζευγαρώνουν σε ηλικία 2 μηνών και στο εξής φέρνουν στον κόσμο άλλα 2 κουνέλια κάθε μήνα. Με βάση αυτή την υπόθεση, μπόρεσε να αποδείξει ότι το σύνολο των σεξουαλικά ώριμων κουνελιών αυξανόταν κάθε μήνα σύμφωνα με μια άπειρη ακολουθία, που αρχίζει ως εξής: 1, 1, 2, 3, 5, 8, 13, 21, 34… Κάθε αριθμός της ακολουθίας ισούται με το άθροισμα των δύο προηγουμένων.  Η «Ακολουθία Fibonacci», όπως ονομάζεται αυτή η σειρά αριθμών, είναι σήμερα γνωστή σε όλους τους μαθηματικούς, επειδή έχει κάποιες ενδιαφέρουσες ιδιότητες. Το 1753, ο μαθηματικός Robert Simpson του Πανεπιστημίου της Γλασκόβης ανακάλυψε, π.χ., ότι ο λόγος δύο διαδοχικών αριθμών στην απειράριθμη αυτή ακολουθία προχωρώντας τείνει όλο και περισσότερο προς το φ. Η χρυσή αναλογία συνδέεται, δηλαδή, με τον πολλαπλασιασμό των κουνελιών, παρόλο που η « Ακολουθία Fibonacci» σχηματίστηκε ανεξάρτητα από την ευκλείδεια γεωμετρία.
Η «Ακολουθία Fibonacci», όπως ονομάζεται αυτή η σειρά αριθμών, είναι σήμερα γνωστή σε όλους τους μαθηματικούς, επειδή έχει κάποιες ενδιαφέρουσες ιδιότητες. Το 1753, ο μαθηματικός Robert Simpson του Πανεπιστημίου της Γλασκόβης ανακάλυψε, π.χ., ότι ο λόγος δύο διαδοχικών αριθμών στην απειράριθμη αυτή ακολουθία προχωρώντας τείνει όλο και περισσότερο προς το φ. Η χρυσή αναλογία συνδέεται, δηλαδή, με τον πολλαπλασιασμό των κουνελιών, παρόλο που η « Ακολουθία Fibonacci» σχηματίστηκε ανεξάρτητα από την ευκλείδεια γεωμετρία.  Παρά τις προσπάθειες του Fibonacci, η χρήση του δεκαδικού συστήματος στην Ευρώπη καθιερώθηκε μόλις τον 17ο αιώνα. Ήδη από την Αναγέννηση, τα μαθηματικά βρίσκονταν σε μεγάλη άνοδο και προόδευαν όσο ποτέ. Οι Ευρωπαίοι μαθηματικοί μετέφεραν την ελληνική λογική και αυστηρότητα σε όλους τους τομείς των μαθηματικών και άγγιξαν νέα επίπεδα αφαίρεσης, αφήνοντας πίσω τους τα μαθηματικά της αρχαιότητας. Το 1509, ο Ιταλός μαθηματικός Luca Pacioli, στο βιβλίο του «De Divina Proportione» (Περί της Θείας Αναλογίας), παρουσίασε 5 επιχειρήματα για το ότι το φ είναι ένας θεϊκός αριθμός. Μεγάλοι ζωγράφοι της Αναγέννησης, όπως ο Botticelli, υιοθέτησαν το φ και χρησιμοποίησαν συνειδητά χρυσά ορθογώνια και χρυσές τομές για να προβάλουν κεντρικά στοιχεία (συχνά ιερά πρόσωπα) στις συνθέσεις τους. Η χρυσή αναλογία εμφανίζεται ακόμα και στη σύγχρονη τέχνη, για παράδειγμα, στον περίφημο πίνακα του Salvador Dali «Ατομική Λήδα», όπου το φ συναντάται σ’ ένα «χρυσό» κανονικό πεντάγωνο με κέντρο τον ομφαλό της Λήδας.
Παρά τις προσπάθειες του Fibonacci, η χρήση του δεκαδικού συστήματος στην Ευρώπη καθιερώθηκε μόλις τον 17ο αιώνα. Ήδη από την Αναγέννηση, τα μαθηματικά βρίσκονταν σε μεγάλη άνοδο και προόδευαν όσο ποτέ. Οι Ευρωπαίοι μαθηματικοί μετέφεραν την ελληνική λογική και αυστηρότητα σε όλους τους τομείς των μαθηματικών και άγγιξαν νέα επίπεδα αφαίρεσης, αφήνοντας πίσω τους τα μαθηματικά της αρχαιότητας. Το 1509, ο Ιταλός μαθηματικός Luca Pacioli, στο βιβλίο του «De Divina Proportione» (Περί της Θείας Αναλογίας), παρουσίασε 5 επιχειρήματα για το ότι το φ είναι ένας θεϊκός αριθμός. Μεγάλοι ζωγράφοι της Αναγέννησης, όπως ο Botticelli, υιοθέτησαν το φ και χρησιμοποίησαν συνειδητά χρυσά ορθογώνια και χρυσές τομές για να προβάλουν κεντρικά στοιχεία (συχνά ιερά πρόσωπα) στις συνθέσεις τους. Η χρυσή αναλογία εμφανίζεται ακόμα και στη σύγχρονη τέχνη, για παράδειγμα, στον περίφημο πίνακα του Salvador Dali «Ατομική Λήδα», όπου το φ συναντάται σ’ ένα «χρυσό» κανονικό πεντάγωνο με κέντρο τον ομφαλό της Λήδας.  ΟΙ ΑΡΙΘΜΟΙ ΠΑΡΑΜΕΝΟΥΝ ΑΙΝΙΓΜΑΤΙΚΟΙ
ΟΙ ΑΡΙΘΜΟΙ ΠΑΡΑΜΕΝΟΥΝ ΑΙΝΙΓΜΑΤΙΚΟΙ
Από τις αρχές του 20ου αιώνα, οι ακέραιοι αριθμοί, οι ρητοί (που μπορούν να γραφούν ως κλάσματα ακεραίων) και οι άρρητοι (που δεν μπορούν να γραφούν ως κλάσματα ακεραίων) ερμηνεύονται με βάση αξιώματα. Ως εκ τούτου, οι μαθηματικοί απέχουν ακόμα πολύ από την πλήρη εξερεύνηση του συστήματος των αριθμών. Μια ολοκληρωμένη κατανόηση των αριθμών θα σήμαινε ότι όλα τα σχετικά με αυτούς προβλήματα θα μπορούσαν να λυθούν, αλλά αυτό μάλλον δεν πρόκειται να συμβεί ποτέ.


 Σύμφωνα με υπολογισμούς, οι παμφάγες μαύρες τρύπες εναλλάσσονται μεταξύ δύο καταστάσεων. Στη μια κατάσταση, το βαρυτικό τους κέντρο (singularity) έχει αρνητική ειδική θερμοχωρητικότητα, κατά την οποία, σε αντίθεση με όποια λογική, γίνονται θερμότερες όσο πιο πολλή ενέργεια χάνουν. Στην άλλη κατάσταση έχουν κανονική θετική θερμοχωρητικότητα.
Σύμφωνα με υπολογισμούς, οι παμφάγες μαύρες τρύπες εναλλάσσονται μεταξύ δύο καταστάσεων. Στη μια κατάσταση, το βαρυτικό τους κέντρο (singularity) έχει αρνητική ειδική θερμοχωρητικότητα, κατά την οποία, σε αντίθεση με όποια λογική, γίνονται θερμότερες όσο πιο πολλή ενέργεια χάνουν. Στην άλλη κατάσταση έχουν κανονική θετική θερμοχωρητικότητα. 

Λεονάρντο Φιμπονάτσι,1170-1240 (Leonardo Pisano Fibonacci)
Με αυτό του το έργο παρουσίασε στη Δυτική Ευρώπη το ινδοαραβικό αριθμητικό σύστημα και τους κανόνες του (1,2,3,4,5,6,7,8,9 και ένα σύμβολο για το μηδέν (0) καθώς και την υποδιαστολή). Επίσης, με ένα πρόβλημα που θέτει στο τρίτο μέρος του Liber abaci καταλήγει στην παρουσίαση της λεγόμενης Ακολουθίας Fibonacci (το όνομα Fibonacci δόθηκε σε αυτή την ακολουθία από το Γάλλο μαθηματικό Edouard Lucas (1842-1891). Η επανέκδοση του Liber Abbaci (1228) με συμπληρωματικά στοιχεία, αφιερώθηκε στον Michael Scott.(β) Practica Geometriae (Πρακτική της Γεωμετρίας), 1220
Tο έργο αυτό είναι αφιερωμένο στον Dominicus Hispanus, ένα ακόμη μέλος της Αυλής του Φρειδερίκου Β’. Περιλαμβάνει γεωμετρικά προβλήματα με θεωρήματα βασισμένα στα Στοιχεία του Ευκλείδη. Αντί για τις αποδείξεις των θεωρημάτων αυτών, στο βιβλίο αναφέρονται πρακτικές πληροφορίες για τη χρήση τους.(γ) Liber Quadratorum (Το Βιβλίο των Τετραγωνικών αριθμών), 1225
Είναι ένα βιβλίο αριθμολογίας, στο οποίο εξετάζει επίσης και μεθόδους εύρεσης πυθαγορικών τριάδων. Αφιερώθηκε στο Φρειδερίκο Β’.
Το βιβλίο αυτό είναι μια συλλογή των λύσεων των προβλημάτων και των τετραγωνικών εξισώσεων με δύο ή περισσότερες μεταβλητές που τέθηκαν στον Fibonacci υπό την παρουσία του Φρειδερίκου από τον Johannes of Palermo, μέλος της Αυλής.
(ε) Γράμμα στον Δάσκαλο Theodorus
στην οποία κάθε αριθμός είναι άθροισμα των δύο προηγούμενων.Η ακολουθία Fibonacci είναι μια βάση για τη γεωμετρία Φράκταλ. Επιπλέον, ο λόγος δύο διαδοχικών αριθμών της ακολουθίας τείνει προς την Χρυσή Τομή ή Χρυσή Αναλογία, ή Χρυσό Αριθμό Φ =1.618033989.Αν και υπάρχουν αναφορές ότι αυτή η ακολουθία είχε αναφερθεί περίπου μισό αιώνα πριν, από τους Ινδούς Gospala και Hemachandra, ο Fibonacci συνάντησε αυτή την ακολουθία μελετώντας την Μεγάλη Πυραμίδα του Χέοπα στην Αίγυπτο, η οποία και είναι χτισμένη με βάση τον αριθμό Φ. Ο Fibonacci πίστευε ότι αυτοί οι αριθμοί μπορούν να ξεκλειδώσουν τα μυστικά της Φύσης. Αυτό μπορούμε να το αντιληφθούμε αν λάβουμε υπόψη πως η ακολουθία του, καθώς και η λογαριθμική σπείρα που δημιουργείται σε σχέση με τον αριθμό Φ, απαντώνται σχεδόν παντού: 1. Βοτανολογία, Βιολογία:
Στην ανάπτυξη των φυτών, στο γενεαλογικό δένδρο της αρσενικής μέλισσας, σε κελύφη σαλιγκαριών, στα κέρατα του κριού, στην ανάπτυξη του ανθρώπου, στα σταυροδρόμια της βιολογίας και των μαθηματικών.2. Φυσικές Επιστήμες:
Στην ατομική σχάση, στην ηλεκτρονική ανάλυση δικτύων, στον προγραμματισμό των Η/Υ, στις διακλαδώσεις των ποταμών, στα κύματα των ωκεανών, στους ανεμοστρόβιλους, στο ηλιακό σύστημα, στους γαλαξίες και άλλα.3. Οικονομία, Εκπαίδευση, Ποίηση, Μουσική:
Στους κύκλους των χρηματαγορών, στην εκπαίδευση μαθητών με δυσκολίες στη μάθηση, στην ανάλυση της ποίησης, σε μουσικά αριστουργήματα.4. Αρχαιολογία, Αρχιτεκτονική, Τέχνη:
Στη Μεγάλη Πυραμίδα του Χέοπα, στη Μινωική αρχιτεκτονική, στον Παρθενώνα της Ακρόπολης Αθηνών, σε μωσαϊκά των αρχαίων Ρωμαίων και άλλα.
 Ο Leonardo Fibonacci ήταν δικαιολογημένα η μεγαλύτερη μαθηματική ιδιοφυΐα του Μεσαίωνα.
Ο Leonardo Fibonacci ήταν δικαιολογημένα η μεγαλύτερη μαθηματική ιδιοφυΐα του Μεσαίωνα.
Με το θάρρος του, με το πνεύμα συγκριτικής έρευνας και φιλομάθειας κατάφερε να ξεκλειδώσει κάποια από τα εσωτερικά μυστικά της φύσης και να φέρει ένα μέρος από το Φως της Ανατολής στη σκοτεινή και μεσαιωνική Δύση.
Ήταν πραγματικά ένας πνευματικά ελκυστικός μαθηματικός που κατόρθωσε να συνδέσει τις θεωρητικές παραδόσεις των Ελλήνων και τις μαθηματικές παραδόσεις των Αράβων, εγκαθιδρύοντάς τους στην Ευρώπη.
Τα γενικότερα επιτεύγματά του αναγνωρίσθηκαν –και αναγνωρίζονται- χωρίς αμφισβήτηση.
Οι αριθμοί Φιμπονάτσι-το αριθμητικό σύστημα της φύσης
Το θέμα της σημερινής εγγραφής θα σχετίζεται με τα μαθηματικά. Συγκεκριμένα θα ασχοληθούμε με τους αριθμούς Fibonacci. 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …….
Oι πρώτοι δύο αριθμοί Φιμπονάτσι είναι το 0 και το 1, και κάθε επόμενος αριθμός είναι το άθροισμα των δύο προηγούμενων.
Επιπλέον, ο λόγος δύο διαδοχικών αριθμών της ακολουθίας Φιμπονάτσι τείνει προς την χρυσή τομή ή χρυσή αναλογία, δηλαδή τον αριθμό φ=1,618033989.
Υπέροχοι και μυστήριοι χαρακτηρίζονται αυτοί οι αριθμοί και απαντώνται παντού και σε διάφορες επιστήμες. Εκπληκτικός όμως είναι ο τρόπος με τον οποίο οι αριθμοί Φιμπονάτσι εμφανίζονται στη φύση.
Είναι το αριθμητικό σύστημα της φύσης. Τους συναντάς παντού, στη διάταξη των φύλλων ενός φυτού, στο μοτίβο των πετάλων ενός λουλουδιού, στο άνθος της αγκινάρας, σε ένα κουκουνάρι ή στο φλοιό ενός ανανά.
Ισχύουν για την ανάπτυξη κάθε ζωντανού οργανισμού, ενός κυττάρου, ενός κόκκου σιταριού, μιας κυψέλης μελισσών, ακόμη και για όλη την ανθρωπότητα.
Φωτογραφία knitalatte11
Μπορούμε να μετρήσουμε στις μαργαρίτες 13, 21, 34, 55, ή και 89 πέταλα. Οι κοινές μαργαρίτες του αγρού έχουν συνήθως 34 πέταλα γεγονός που σίγουρα επηρεάζει το αποτέλεσμα του παιχνιδιού «μ’ αγαπά δεν μ’ αγαπά». Ο κρίνος έχει τρία πέταλα, ηνεραγκούλα έχει πέντε, κ.λ.π.
Σίγουρα, αυτός ο συνδυασμός φύσης και μαθηματικών δεν είναι τυχαίος!! Άραγε, τα μαθηματικά αντιγράφουν τη φύση ή η φύση τα μαθηματικά; Δεν συμφωνείτε όμως μαζί μου ότι είναι εκπληκτικός ο τρόπος που συνδυάζονται, όπως και το αποτέλεσμα;
Στο πλαίσιο του προγράμματος, που πραγματοποιήθηκε υπό την αιγίδα του Μουσείου Επιστήμης και Βιομηχανίας του Μάντσεστερ, εκατοντάδες εθελοντές σε όλο τον κόσμο καλλιέργησαν ηλιοτρόπια.
Η επιστημονική έρευνα στηρίχθηκε στη θεωρία του παγκοσμίου φήμης Bρετανού μαθηματικού, καθηγητή λογικής και κρυπτογράφου Άλαν Μάθισον Τούρινγκ (1912-1954), ο οποίος θεωρείται πατέρας της επιστήμης των υπολογιστών και απέδειξε ότι οι σπείρες που σχηματίζουν οι σπόροι στα άνθη αναπαράγουν μαθηματικά μοντέλα.
Για τους σκοπούς του προγράμματος συλλέχθηκαν στοιχεία από 557 ηλιοτρόπια από επτά χώρες.
Το 82% των λουλουδιών ακολούθησε περίπλοκες μαθηματικές δομές, συμπεριλαμβανομένης της ακολουθίας Φιμπονάτσι, στην οποία ο κάθε αριθμός αποτελεί άθροισμα των δύο προηγούμενων (0,1,1,2,3,5,8,13,21 κ.ο.κ).
Ο Τούρινγκ και οι επιστημονικοί επίγονοί του προσπάθησε να αποδείξει ότι οι σπείρες στα ηλιοτρόπια αναπαράγουν την ακολουθία Φιμπονάτσι.
Τώρα, μαθηματικοί και βιολόγοι θα συνεργαστούν για να κατανοήσουν εις βάθος τις προεκτάσεις των μαθηματικών δομών στους φυτικούς οργανισμούς.
Το πείραμαΕκατοντάδες εθελοντές δέχθηκαν να συμμετάσχουν στο πρόγραμμα «Τα Ηλιοτρόπια του Τιούρινγκ», του οποίου ο δικτυακός τόπος ζητά από το κοινό να καλλιεργήσει ηλιοτρόπια και να μετρήσει τις σπείρες που σχηματίζουν οι σπόροι δεξιόστροφα και αριστερόστροφα. 
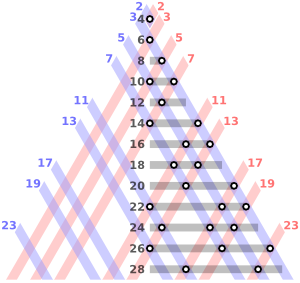
Όπως αναφέρει από το φεστιβάλ στο Μάντσεστερ η Έιμι Φρίμπορν του Yahoo UK!, η ανάλυση των μετρήσεων σε 557 ηλιοτρόπια σε επτά χώρες δείχνει ότι ο κώδικας Φιμπονάτσι εμφανίζεται στο 82% των περιπτώσεων.Το ενδιαφέρον είναι ότι σε 26 ηλιοτρόπια παρατηρήθηκαν διπλές αλληλουχίες Φιμπονάτσι, και 33 άλλες περιπτώσεις εμφάνιζαν την αλληλουχία Λούκας.
Η αλληλουχία αυτή είναι παρόμοια με του Φιμπονάτσι, με την έννοια ότι κάθε αριθμός είναι άθροισμα των δύο προηγούμενων, ωστόσο ξεκινάει ως 2, 1, 3, 4, 7, 11, 18, 29 κ.ο.κ.
Το ανορθόδοξο ανοιχτό πείραμα διοργανώθηκε από το Φεστιβάλ Επιστήμης του Μάντσεστερ και το Μουσείο Επιστήμης και Βιομηχανίας του Μάντσεστερ, προκειμένου να τιμήσουν τον ένα αιώνα από τη γέννηση του Τιούρινγκ.
Ποιος ήταν ο Άλαν Τούρινγκ
Ο Άλαν Τούρινγκ είχε τεράστια συμβολή στη νίκη των συμμαχικών δυνάμεων επί των Γερμανών κατά τον Β’ Παγκόσμιο Πόλεμο, καθώς είχε κεντρικό ρόλο στην αποκωδικοποίηση της Γερμανικής κρυπτογραφικής συσκευής Enigma.
Η εργασία του Τούρινγκ κρατήθηκε μυστική μέχρι τη δεκαετία του ’70, ακόμη και οι στενοί φίλοι του δεν την ήξεραν.
Συνέβαλε με διάφορες μαθηματικές ιδέες για την αποκρυπτογράφηση μηνυμάτων των συσκευών Enigma και Lorenz SZ 40/42.
Στο Μπλέτσλεϊ Παρκ ο Τούρινγκ εργάστηκε από το 1939 ως το 1940 όταν και μετακινήθηκε προς την Ομάδα 8.
Ο Τούρινγκ συνειδητοποίησε ότι δεν ήταν απαραίτητο να εξεταστούν όλοι οι πιθανοί συνδυασμοί για να σπάσουν τους κωδικούς της μηχανής Enigma.
Απέδειξε ότι ήταν δυνατό να εξετάσει τις σωστές τοποθετήσεις των διακοπτών (περίπου ένα εκατομμύριο συνδυασμοί) χωρίς να πρέπει να εξεταστούν οι τοποθετήσεις του πίνακα συνδέσεων (περίπου 157 εκατομμύριο συνδυασμοί).
To γεγονός αυτό εκτιμάται ότι έσωσε εκατομμύρια ζωές και συνέβαλε στην ταχύτερη πτώση του Χίτλερ.

Μετά τον πόλεμο, ο Τούρινγκ ασχολήθηκε με το θέμα της τεχνητής νοημοσύνης (αν δηλαδή μια μηχανή μπορεί να θεωρηθεί ότι γνωρίζει και μπορεί να σκεφτεί) και πρότεινε ένα πείραμα γνωστό σήμερα ως δοκιμή Τούρινγκ για τον καθορισμό των κριτηρίων της:
Ένας υπολογιστής είναι πράγματι νοήμων αν και μόνο αν κάποιος άνθρωπος δεν μπορεί να καταλάβει τη διαφορά ανάμεσα στις απαντήσεις του και σε αυτές ενός άλλου ανθρώπου σε γενικές ερωτήσεις.
Επίσης, με την καθολική μηχανή Τούρινγκ παρείχε μια επίσημη έννοια του αλγορίθμου και των υπολογίσιμων αριθμών διατυπώνοντας την ευρέως αποδεκτή έκδοση Τούρινγκ, ότι δηλαδή οποιοδήποτε πρακτικό πρότυπο υπολογισμού έχει είτε ένα ισότιμο είτε ένα υποσύνολο των ικανοτήτων μιας μηχανής Τούρινγκ.
Αργότερα σχεδίασε έναν από τους πρώτους ηλεκτρονικούς προγραμματίσιμους ψηφιακούς υπολογιστές στο εθνικό φυσικό εργαστήριο. Το Βραβείο Τούρινγκ που θεωρείται ως το αντίστοιχο του Νόμπελ στον κόσμο των υπολογιστών δημιουργήθηκε προς τιμήν του.
Ο Τούρινκ έπεσε θύμα της ανθρώπινης βλακείας και μισαλλοδοξίας καθώς το 1952 υποχρεώθηκε σε ορμονικής θεραπείας για τη μείωση της λίμπιντο, εξαιτίας της ομοφυλοφιλίας του.
Επέλεξε τις εγχύσεις ορμονών οιστρογόνων, οι οποίες διήρκεσαν ένα έτος, με παρενέργειες όπως η ανάπτυξη στήθους.
Το 1954 πέθανε από δηλητηρίαση από κυάνιο, προφανώς από ένα μήλο που άφησε μισοφαγωμένο και περιείχε κυάνιο.
Ανακαιφαλαίωση:
Ο αριθμός 1,618 ως τώρα περνούσε απαρατήρητος χωρίς να γνωρίζουμε την πολυσχιδή εφαρμογή του.
Ωστόσο διαπιστώνουμε ότι η εφαρμογή του ξεκινά από την αναλογία της φύσης, του προσώπου μας, του σώματός μας…περνά στην τέχνη, στους ζωντανούς οργανισμούς και πολλά άλλα που πιθανόν να μην έχουν παρατηρηθεί.
Αν μετρήσεις τις μέλισσες σε μια κυψέλη οπουδήποτε στον κόσμο θα παρατηρήσεις ότι η αναλογία των θηλυκών προς των αρσενικών μελισσών καταλήγει πάντα σε έναν αριθμό…
Αν μετρήσεις την απόσταση από την κορυφή του κεφαλιού μέχρι το πάτωμα και τη διαιρέσεις με την απόσταση από τον αφαλό μέχρι το πάτωμα προκύπτει πάντα ο ίδιος αριθμός…
Αν μετρήσεις την απόσταση από τον ώμο μέχρι τις άκρες των δακτύλων και τη διαιρέσεις με την απόσταση από τον αγκώνα μέχρι τις άκρες των δακτύλων προκύπτει πάντα ο ίδιος αριθμός…
…ο αριθμός αυτός είναι ο 1,618 ή ο γνωστός αριθμός φ!!!
Μήπως τελικά είχε δίκιο ο Λεονάρντο Ντα Βίντσι που πίστευε στη Θεία Αναλογία?
Πόσοι από εσάς ακόμα πιστεύουν στις συμπτώσεις?