Ο αριστοτελικός νόμος της κίνησης

Θα εξετάσουμε την αριστοτελική φυσική της κίνησης για τα γήινα σώματα. Ο Αριστοτέλης έλεγε ότι σε κάθε είδους κίνηση υπάρχουν δυο βασικοί παράγοντες: η κινούσα δύναμη, την οποία συμβολίζουμε με F, και η αντίσταση, την οποία συμβολίζουμε με R. Σύμφωνα με τον Αριστοτέλη, για να υπάρξει κίνηση πρέπει η κινούσα δύναμη να είναι μεγαλύτερη από την αντίσταση. Συνεπώς, η πρώτη αρχή μας για την κινούσα δύναμη είναι

δηλαδή η δύναμη πρέπει να είναι μεγαλύτερη από την αντίσταση. Στη συνέχεια ας εξετάσουμε την επίδραση διαφορετικών αντιστάσεων, διατηρώντας την κινούσα δύναμη σταθερή.Το πείραμά μας θα γίνει με την πτώση σωμάτων, τα οποία αφήνονται να πέσουν ελεύθερα, ξεκινώντας από την ηρεμία, μέσα σε υλικά μέσα διαφορετικής αντίστασης. Για να διατηρήσουμε τις συνθήκες σταθερές όλα τα πίπτοντα σώματα είναι σφαίρες, έτσι ώστε η επίδραση του σχήματος στην κίνησή τους να είναι ίδια. Φυσικά, ο Αριστοτέλης γνώριζε καλά ότι η ταχύτητα ενός σώματος – εάν οι υπόλοιποι παράγοντες είναι ίδιοι εξαρτάται γενικά από το σχήμα του.

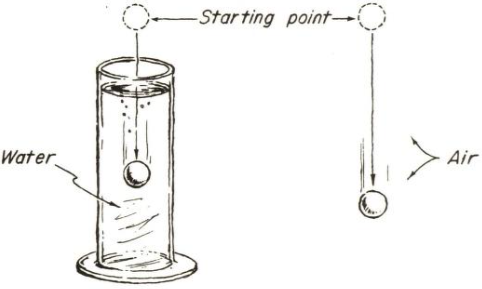
Ας δούμε τώρα το πείραμα. Θα χρησιμοποιήσουμε δύο χαλύβδινες ίδιου σχήματος, μεγέθους, και βάρους. Θα τις αφήσουμε να πέσουν ταυτόχρονα, η μία μέσα σε αέρα και η άλλη μέσα σε νερό. Για να κάνετε αυτό το πείραμα θα χρειαστείτε έναν μακρύ κύλινδρο γεμάτο με νερό. Κρατήστε τις δύο σφαίρες τη μια δίπλα στην άλλη, τη μια πάνω από το νερό και την άλλη δίπλα σε αυτή τη στήλη του νερού. Όταν τις αφήσετε ταυτόχρονα, θα διαπιστώσετε ότι η ταχύτητα αυτής που κινείται στον αέρα είναι αναμφίβολα πολύ μεγαλύτερη από την ταχύτητα εκίνης που πέφτει μέσα στο νερό.

Όταν τις αφήσετε ταυτόχρονα , θα διαπιστώσετε ότι η ταχύτητα αυτής που κινείται στον αέρα είναι αναμφίβολα πολύ μεγαλύτερη από την ταχύτητα εκείνης που πέφτει μέσα στο νερό. Για να αποδείξουμε ότι τα αποτελέσματα του πειράματος δεν οφείλονται στο γεγονός ότι οι σφαίρες είναι χαλύβδινες ή ότι έχουν ένα συγκεκριμένο βάρος, μπορούμε να το επαναλάβουμε χρησιμοποιώντας είτε μικρότερες χαλύβδινες σφαίρες, ένα ζευγάρι γυάλινες ή μπρούτζινες σφαίρες κ.ο.κ. Σε μικρότερη κλίμακα, ο καθένας θα μπορούσε να επαναλάβει αυτό το πείραμα χρησιμοποιώντας είτε δυο γυάλινους βόλους και ένα ψηλό ποτήρι γεμάτο με νερό μέχρι το χείλος του. Το αποτέλεσμα αυτού του πειράματος μπορεί να γραφτεί υπό την μορφή εξίσωσης, στην οποία εκφράζουμε το γεγονός ότι – εάν όλοι οι υπόλοιποι παράγοντες είναι ίδιοι – η ταχύτητα στο νερό (το οποίο αντιστέκεται ή αλλιώς παρεμποδίζει πολύ την κίνηση) είναι μικρότερη από την ταχύτητα στον αέρα (ο οποίος δεν παρεμποδίζει την κίνηση όσο το νερό):

δηλαδή η ταχύτητα είναι αντιστρόφως ανάλογη προς την αντίσταση του υλικού εντός του οποίου κινείται το σώμα. Το ότι το νερό αντιστέκεται στην κίνηση είναι γνωστό σε όλους μας από την εμπειρία μας. Όποιος έχει προαπαθήσει να τρέξει μέσα στο νερό της θάλασσας γνωρίζει πόσο πολύ το νερό αντιστέκεται στην κίνησή του σε σχέση με τον αέρα.

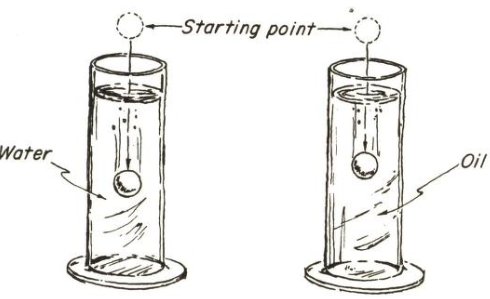
Ας κάνουμε τώρα το πείραμα με δύο κυλινδρικούς σωλήνες, ο ένας γεμάτος με νερό και ο άλλος γεμάτος με λάδι.

Το λάδι αντιστέκεται στην κίνηση ακόμα περισσότερο απ’ ότι το νερό. Όταν οι δυο πανομοιότυπες χαλύβδινες μπάλες αφεθούν να πέσουν την ίδια στιγμή, αυτή που πέφτει μέσα στο νερό θα φτάσει στον πυθμένα πολύ πριν από εκείνη που πέφτει μέσα στο λάδι. Επειδή η αντίσταση R_λ του λαδιού είναι πολύ μεγαλύτερη από την αντίσταση R_ν του νερού, μπορούμε να προβλέψουμε ότι αν οποιαδήποτε δυο πανομοιότυπα αντικείμενα αφεθούν να πέσουν μέσα σε αυτά τα υγρά, αυτό που πέφτει μέσα στο νερό θα διανύσει μια συγκεκριμένη απόσταση ταχύτερα από εκείνο που πέφτει μέσα στο λάδι. Αυτή η πρόβλεψη μπορεί να επιβεβαιωθεί πολύ εύκολα. Στη συνέχεια, αφού έχει βρεθεί ότι η αντίσταση του νερού, R_ν, είναι μεγαλύτερη από την αντίσταση του αέρα, R_α,
R_λ > R_ν
R_ν> R_α
πρέπει και η αντίσταση του λαδιού να είναι μεγαλύτερη από την αντίσταση του αέρα
R_λ>R_α
Αυτό μπορούμε επίσης να το επαληθεύσουμε επαναλαμβάνοντας το αρχικό πείραμα με έναν κύλινδρο γεμάτο με λάδι αντί για νερό.

Στη συνέχεια, ας παρατηρήσουμε την επίδραση διαφορετικών κινουσών δυνάμεων. Σε αυτό το πείραμα χρησιμοποιούμε πάλι τον μακρύ κύλινδρο γεμάτο με νερό. Ρίχνουμε μέσα ταυτόχρονα μια μικρή και μια μεγάλη χαλύβδινη μπάλα. Βλέπουμε ότι η μεγάλη χαλύβδινη μπάλα, η πιο βαριά από τις δυο, φτάνει στον πυθμένα πριν από την ελαφρύτερη. Εδώ θα έλεγε κανείς ότι το μέγεθος θα μπορούσε να παίζει κάποιο ρόλο, αλλά η μεγάλη μπάλα θα πρέπει αντιθέτως να συναντά μεγαλύτερη αντίσταση απ’ ότι η μεγαλύτερη. Άρα μπορεί να θεωρηθεί ότι το πείραμα δείχνει ότι όσο μεγαλύτερη είναι η δύναμη που ασκείται για να υπερνικηθεί μια συγκεκριμένη αντίσταση, τόσο μεγαλύτερη θα είναι η ταχύτητα. Αυτό το πείραμα μπορεί να επαναληφθεί, αυτή τη φορά με μια χαλύβδινη μπάλα και μια γυάλινη, έτσι ώστε να έχουν και οι δύο το ίδιο μέγεθος αλλά διαφορετικά βάρη. Για άλλη μια φορά, βρίσκουμε ότι η πιο βαριά μπάλα φαίνεται να είναι πιο ικανή να υπερνικήσει την αντίσταση του υλικού μέσου. Έτσι, φτάνει πρώτη στον πυθμένα ή, με άλλα λόγια, αποκτά μεγαλύτερη ταχύτητα. Το ίδιο πείραμα μπορεί να γίνει μέσα σε λάδι και σε διάφορα άλλα υγρά (οινόπνευμα, γάλα, κ.λπ.). Το γενικό αποτέλεσμα που θα προκύψει είναι το ίδιο. Σε μορφή εξίσωσης, μπορούμε να δηλώσουμε τα συμπεράσματα του πειράματος ως εξής:

ή, εάν όλοι οι υπόλοιποι παράγοντες είναι ίδιοι, όσο μεγαλύτερη είναι η δύναμη τόσο μεγαλύτερη είναι η ταχύτητα.
Μπορούμε τώρα να συνδυάσουμε τις εξισώσεις (1) και (2) σε μια εξίσωση ως εξής:

δηλαδή, η ταχύτητα είναι ανάλογη προς την κινούσα δύναμη και αντιστρόφως ανάλογη προς την αντίσταση του υλικού μέσου ή
η ταχύτητα είναι ανάλογη προς το πηλίκο της δύναμης δια την αντίσταση. Η εξίσωση (3) είναι γνωστή ως ο αριστοτελικός νόμος της κίνησης (*). Πρέπει να σημειωθεί ότι ο ίδιος ο Αριστοτέλης δεν έγραψε τα αποτελέσματά του με μορφή εξισώσεων, δηλαδή με τον σύγχρονο τρόπο έκφρασης τέτοιων σχέσεων. (…..)
(Τα παραπάνω είναι ένα απόσπασμα από το βιβλίο του I. Bernard Cohen, «Η Γέννηση μιας Νέας Φυσικής», Μετάφραση: Μανώλης Καρτσωνάκης, Πανεπιστημιακές Εκδόσεις Κρήτης. Τα σχήματα είναι από την αγγλική έκδοση ΕΔΩ: I. Bernard Cohen, «The birth of a new physics».)

(*) Η «θεμελιώδης εξίσωση» του Αριστοτέλη υ=F/R μπορεί να «προκύψει» και από τη Νευτώνεια μηχανική, όταν η δύναμη της αντίστασης είναι ανάλογη της ταχύτητας F_R=R∙υ και ο συντελεστής αναλογίας R έχει μεγάλη τιμή. Τότε, αν ασκηθεί μια σταθερή δύναμη F στο σώμα, η ταχύτητά του αυξάνεται πολύ γρήγορα και μαζί μ’ αυτή η δύναμη της αντίστασης. Σχεδόν αμέσως, η συνισταμένη δύναμη γίνεται μηδέν ΣF=F-F_R=0, οπότε F=R∙υ ή υ=F/R. H σταθερή ταχύτητα που προκύπτει, συνήθως ονομάζεται οριακή ταχύτητα.

(Η συνέχεια είναι ‘βγαλμένη’ από τον διάλογο Δάσκαλου και Μαθητή που εκτυλίσσεται στο βιβλίο του Στέφανου Τραχανά, «Το Φάντασμα της Όπερας», ΠΕΚ)
Παρότι ο Αριστοτέλης ήταν ο άνθρωπος με την μεγαλύτερη επίδραση στην ιστορία των ιδεών, η θεωρία του για την πτώση των σωμάτων αποτελεί την μακροβιότερη πλάνη στην ιστορία της επιστήμης. Υποστήριζε ότι τα βαριά σώματα πέφτουν πιο γρήγορα όσο μεγαλύτερο είναι το βάρος τους (η δύναμη F στην ‘θεμελιώδη εξίσωσή’ του). Και δεν χρειάζεται βέβαια να ανέβουμε στον πύργο της Πίζας για να απορρίψουμε αυτόν τον ισχυρισμό.

Αρκεί να κρατήσω στο ένα χέρι τα κλειδιά μου, που είναι περίπου πέντε φορές βαρύτερα από το μολύβι που θα κρατήσω στο άλλο. Κι όμως – με την χονδροειδή ακρίβεια με την οποία μπορώ να παρατηρήσω την πτώση τους – βλέπω ότι φτάνουν ταυτόχρονα στο έδαφος, αν τα αφήσω να πέσουν από το ίδιο ύψος. Τι να πιστέψω λοιπόν, τα μάτια μου ή τον Αριστοτέλη;

Πως είναι δυνατόν να άντεξε επί περίπου δυο χιλιάδες χρόνια μια θεωρία η οποία βρίσκεται σε τόσο προκλητική αντίθεση με την εμπειρία;
Η δύναμη του δόγματος, είναι μια ερμηνεία. Δεν υπάρχει τίποτε που να παραλύει τη σκέψη των ανθρώπων – ακόμα και των πιο έξυπνων – τόσο αποτελεσματικά, όσο το δέος απέναντι σ’ ένα δόγμα που υψώνεται μεγαλοπρεπές και δυσθεώρητο απέναντί τους. Πολύ περισσότερο αν στέκεται πίσω του κι ένα άλλο δόγμα – ένα υπερκόσμιο δόγμα – ασύγκριτα πιο παραλυτικό για τη σκέψη απ’ ότι κάθε κοσμικό του ανάλογο. Διότι το αριστοτελικό «σύστημα του κόσμου» δεν απέφυγε τελικά τη συνήθη μοίρα όλων των μεγάλων «συστημάτων». Κατέληξε δόγμα στενά συνδεδεμένο με την Καθολική Εκκλησία και την ανάγκη της να οικοδομήσει μια χριστιανική θεολογία πάνω σε ισχυρές φιλοσοφικές βάσεις.

Αρκεί όμως μόνο η επίκληση της βαριάς σκιάς του δόγματος για να εξηγηθεί η απίστευτη μακροβιότητα μιας θεωρίας σε τόσο εμφανή διάσταση με την πραγματικότητα; Περιείχε η αριστοτελική θεωρία της ελεύθερης πτώσης κάποιου είδους ευλογοφάνεια – μέσα στο πλάισιο του ασριστοτελικού συστήματος ιδεών βεβαίως – που την έκαναν να φαίνεται τόσο φυσιολογική, ώστε να απενεργοποιείται κάθε διάθεση εμπειρικής αμφισβήτισής της επί δυο χιλιάδες χρόνια;

Ας επαναλάβουμε το πείραμα της ελεύθερης πτώσης που κάναμε προηγουμένως, αλλά να ακουμπίσουμε στην μία παλάμη μας (αντί για τα κλειδιά) μια πέτρα βάρους τουλάχιστον 2 κιλών και στην άλλη ένα πετραδάκι όχι περισσότερο από 200 γραμμάρια. Κλείνουμε τα μάτια μας, αδειάζουμε το μυαλό μας από ετοιματζίδικες απαντήσεις και αναρωτιόμαστε τι θα συμβεί αν αφήσουμε τις πέτρες να πέσουν ταυτόχρονα προς το έδαφος. Μήπως η αυθόρμητη απάντησή μας συμφωνεί με την αριστοτελική θεωρία; Αν κάνετε το ίδιο πείραμα και με άλλους ανθρώπους, που δεν έχουν έτοιμες απαντήσεις στο μυαλό τους θα πάρετε πάλι την «αριστοτελική» απάντηση -η μεγάλη πέτρα θα φτάσει πολύ πιο γρήγορα στο έδαφος. Κι όταν ανοίγουμε τα μάτια μας και αφήνουμε τις πέτρες να πέσουν … μας φαίνεται απίστευτο καθώς τις βλέπουμε να φτάνουν ταυτόχρονα στο έδαφος.

Που οφείλεται η λανθασμένη πρόβλεψη; Αφού αισθανόμαστε την βαριά πέτρα να πιέζει πολύ περισσότερο το χέρι μας, φαίνεται πως το «θέλει» πολύ περισσότερο να πάει προς τα κάτω, σε σύγκριση με την ελαφρότερη που δεν δείχνει να το «θέλει» τόσο πολύ. Επομένως, αφού το «θέλει» πολύ περισσότερο θα φτάσει πολύ πιο γρήγορα στο έδαφος. Πρόκειται για μια καθαρά ανθρωποκεντρική θεώρηση – φτάνει πολύ πιο γρήγορα στον στόχο του όποιος τον «επιθυμεί» περισσότερο. Αν και Αριστοτέλης δεν αναγνώριζε επιθυμίες στα άψυχα πράγματα. Μόνο τέλη. Γι’ αυτό και η φυσική του χαρακτηρίζεται τελεολογική. Στην περίπτωση της ελεύθερης πτώσης, για παράδειγμα, θεωρούσε ότι τα βαριά σώματα πάνε προς τα κάτω – δηλαδή προς τη γη – απλώς επειδή εκεί είναι ο φυσικός τους τόπος. Κι όταν τον φτάσουν, η κίνηση σταματάει. Επέρχεται το τέλος της κίνησης.

Μπορούμε να πούμε ότι μακροβιότητα της αριστοτελικής θεωρίας για την κίνηση οφείλεται στους εξής τρεις παράγοντες: α) στην παραλυτική επιβολή του δόγματος β) στην ισχυρή ευλογοφάνεια της ίδιας της θεωρίας, και γ) στον άκρως αντιδιαισθητικό χαρακτήρα της αρχής της αδράνειας ο οποίος έκανε εξαιρετικά δύσκολη την ανακάλυψή της.

Κλείνοντας, αξίζει να σημειωθεί ότι ο αριστοτελικός νόμος της κίνησης δεν συμφωνεί με την ατομική θεωρία. Μέσα στο κενό η αντίσταση στην κίνηση των ατόμων – δηλαδή το R στον τύπο του Αριστοτέλη – μηδενίζεται και, όπως ξέρουμε από τα μαθηματικά όταν ο παρονομαστής ενός κλάσματος γίνει μηδέν το κλάσμα απειρίζεται. Επομένως τα άτομα είναι … καταδικασμένα να κινούνται συνεχώς με άπειρη ταχύτητα, το οποίο είναι, προφανώς παράλογο.

Επομένως, η πολεμική του Αριστοτέλη εναντίον των ατομικών φιλοσόφων ήταν μια γνήσια επιστημονική διαμάχη κι όχι μια αερο-μαχία μεταξύ πολιτικών παρατάξεων. Ο διάλογος ανάμεσα στις διαφορετικές σχολές σκέψης του αρχαίου ελληνικού κόσμου μπορεί να είχε συχνά πολεμικό χαρακτήρα, ήταν όμως πάντα διάλογος με αυστηρά λογικά επιχειρήματα. Γι’ αυτό εξάλλου και η διαλεκτική – αναζήτηση της αλήθειας μέσω του διαλόγου – θεωρείται μια κατ’ εξοχήν ελληνική τέχνη. Ένα σπουδαίο κομμάτι κι αυτή της μεγάλης ελληνικής κληρονομιάς. Από την οποία, βέβαια, εμείς εδώ συζητάμε μόνο μια μικρή γωνίτσα της. Αυτήν που έχει να κάνει με τη φυσική επιστήμη.

Πηγή…